Surgery structure set
In mathematics, the structure set 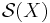 is the basic object in the study of manifolds which are homotopy equivalent to a closed manifold X. It is a concept which helps to answer the question whether two homotopy equivalent manifolds are diffeomorphic (or PL-homeomorphic or homeomorphic). There are different versions of the structure set depending on the category (DIFF, PL or TOP) and whether Whitehead torsion is taken into account or not.
is the basic object in the study of manifolds which are homotopy equivalent to a closed manifold X. It is a concept which helps to answer the question whether two homotopy equivalent manifolds are diffeomorphic (or PL-homeomorphic or homeomorphic). There are different versions of the structure set depending on the category (DIFF, PL or TOP) and whether Whitehead torsion is taken into account or not.
Contents[hide] |
Definition
Let X be a closed smooth (or PL- or topological) manifold of dimension n. We call two homotopy equivalences 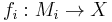 from closed manifolds
from closed manifolds 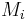 of dimension
of dimension  to
to  (
(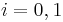 ) equivalent if there exists a cobordism
) equivalent if there exists a cobordism 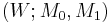 together with a map
together with a map ![(F;f_0,f_1): (W;M_0,M_1) \to (X \times [0,1];X \times \{0\},X \times \{1\})](/2012-wikipedia_en_all_nopic_01_2012/I/61cb0e29a9fd164bb73413f7c0a061d9.png) such that
such that  ,
, 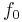 and
and 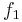 are homotopy equivalences. The structure set
are homotopy equivalences. The structure set 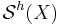 is the set of equivalence classes of homotopy equivalences
is the set of equivalence classes of homotopy equivalences 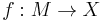 from closed manifolds of dimension n to X. This set has a preferred base point:
from closed manifolds of dimension n to X. This set has a preferred base point: 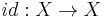 .
.
There is also a version which takes Whitehead torsion into account. If we require in the definition above the homotopy equivalences F, 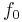 and
and 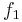 to be simple homotopy equivalences then we obtain the simple structure set
to be simple homotopy equivalences then we obtain the simple structure set 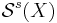 .
.
Remarks
Notice that 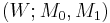 in the definition of
in the definition of 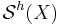 resp.
resp. 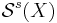 is an h-cobordism resp. an s-cobordism. Using the s-cobordism theorem we obtain another description for the simple structure set
is an h-cobordism resp. an s-cobordism. Using the s-cobordism theorem we obtain another description for the simple structure set 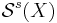 , provided that n>4: The simple structure set
, provided that n>4: The simple structure set 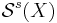 is the set of equivalence classes of homotopy equivalences
is the set of equivalence classes of homotopy equivalences 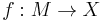 from closed manifolds
from closed manifolds  of dimension n to X with respect to the following equivalence relation. Two homotopy equivalences
of dimension n to X with respect to the following equivalence relation. Two homotopy equivalences 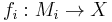 (i=0,1) are equivalent if there exists a diffeomorphism (or PL-homeomorphism or homeomorphism)
(i=0,1) are equivalent if there exists a diffeomorphism (or PL-homeomorphism or homeomorphism) 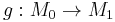 such that
such that 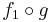 is homotopic to
is homotopic to 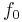 .
.
As long as we are dealing with differential manifolds, there is in general no canonical group structure on 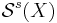 . If we deal with topological manifolds, it is possible to endow
. If we deal with topological manifolds, it is possible to endow 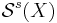 with a preferred structure of an abelian group (see chapter 18 in the book of Ranicki).
with a preferred structure of an abelian group (see chapter 18 in the book of Ranicki).
Notice that a manifold M is diffeomorphic (or PL-homeomorphic or homeomorphic) to a closed manifold X if and only if there exists a simple homotopy equivalence 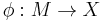 whose equivalence class is the base point in
whose equivalence class is the base point in  . Some care is necessary because it may be possible that a given simple homotopy equivalence
. Some care is necessary because it may be possible that a given simple homotopy equivalence  is not homotopic to a diffeomorphism (or PL-homeomorphism or homeomorphism) although M and X are diffeomorphic (or PL-homeomorphic or homeomorphic). Therefore, it is also necessary to study the operation of the group of homotopy classes of simple self-equivalences of X on
is not homotopic to a diffeomorphism (or PL-homeomorphism or homeomorphism) although M and X are diffeomorphic (or PL-homeomorphic or homeomorphic). Therefore, it is also necessary to study the operation of the group of homotopy classes of simple self-equivalences of X on 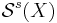 .
.
The basic tool to compute the simple structure set is the surgery exact sequence.
Examples
Topological Spheres: The generalized Poincaré conjecture in the topological category says that 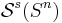 only consists of the base point. This conjecture was proved by Smale (n > 4), Freedman (n = 4) and Perelman (n = 3).
only consists of the base point. This conjecture was proved by Smale (n > 4), Freedman (n = 4) and Perelman (n = 3).
Exotic Spheres: The classification of exotic spheres by Kervaire and Milnor gives 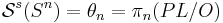 for n > 4 (smooth category).
for n > 4 (smooth category).
References
- Browder, William (1972), Surgery on simply-connected manifolds, Berlin, New York: Springer-Verlag, MR0358813
- Ranicki, Andrew (2002), Algebraic and Geometric Surgery, Oxford Mathematical Monographs, Clarendon Press, ISBN 978-0-19-850924-0, MR2061749, http://www.maths.ed.ac.uk/~aar/books/index.htm
- Wall, C. T. C. (1999), Surgery on compact manifolds, Mathematical Surveys and Monographs, 69 (2nd ed.), Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-0942-6, MR1687388
- Ranicki, Andrew (1992), Algebraic L-theory and topological manifolds, Cambridge Tracts in Mathematics 102, CUP, ISBN 0-521-42024-5, MR1211640, http://www.maths.ed.ac.uk/~aar/books/topman.pdf